量化
量化方法的分类
- 对称性:非对称量化、对称量化
- 均匀性:均匀量化、非均匀量化
- 训练后量化(PTQ)、量化感知训练(QAT)
- 动态量化、静态量化
- 线性量化、非线性量化
对于量化来说,我们需要保证模型推理过程中(例如可以提高bachsize),计算时间占主导地位,而不是读数据、写数据占主要时间。这样我们使用量化就能明显地加速,否则可能量化之后和没量化的时间差距并不大
量化的计算方法
最常用的是仿射量化(Affine Quantization),也称为线性量化(Linear Quantization)*或*非对称量化(Asymmetric Quantization)。其核心思想是将一个浮点数范围 [r_min, r_max] 线性地映射到一个整数范围 [q_min, q_max]。
有符号整数和无符号整数的范围不一样
- 量化公式:
q = clamp(round(r/S + Z), qmin, qmax)
- r: 原始的FP32浮点数。这可以是一个模型的权重(Weight)或者一个激活值(Activation)。
- q:量化后的整数
- S:(Scale-缩放因子)
- FP32浮点数
- 它定义了量化表示中,一个整数单位(步长)对应多少真实的浮点值范围,S越小,则表示精度越高
- S = (r_max - r_min) / (q_max - q_min)
r_max: 需要量化的这组FP32数值中的最大值。
r_min: 需要量化的这组FP32数值中的最小值。
q_max: 目标整数类型的最大值 (例如,INT8为127)。
q_min: 目标整数类型的最小值 (例如,INT8为-128)。
- Z( Zero-point- 零点)
- 它指定了原始浮点值 0.0 应该映射到哪个整数值
- 引入零点是为了能够准确地表示非对称的浮点数范围(即r_min和r_max关于0不对称)以及原始的浮点值0.0。如果原始浮点范围恰好关于0对称,并且目标整数范围也关于0对称,理论上零点可以是0,但这并不总是最优或可行。
- Z = round(q_max - r_max / S) 或者(等价地,但在实践中更常用以避免浮点精度问题) Z = q_min - round(r_min / S)
反量化公式: r = S(q − Z)
为什么存在量化误差?
从上面的公式中可以看出,我们在量化的过程中进行了round函数的计算,对float进行了取整,模型量化精度损失的主要原因为量化-反量化(quantization-dequantization)过程中取整引起的误差。
模型经过量化后,在推理框架(e.g. TensorRT、Openvino)运行时,会根据不同的Op调用相应的算子:
- 某些算子可以支持低精度的输入输出(e.g Conv、Relu、Gelu),此时推理框架会调用INT8 kernel 进行计算;
- 某些算子需要高精度输入输出(使用低精度会导致误差显著增加),那么将会将INT8输入反量化为FP32浮点数之后再输入算子进行计算
量化训练的关键:
量化的重点在于确定S,Z。更具体来说是确定r_max,r_min
量化的粒度:
- Per-Tensor: 对整个tensor(例如一个卷积层的所有channel的权重)使用同一对S 和 Z(即S,Z是基于这整个tensor计算而来的)(实现简单,开销小)
- Per-Channel(或者Per-Axis):对tensor对某个维度(例如,卷积核的输出通道维度)分别计算S,Z,这样可以为不同通道设置更合适的量化范围,通常能带来更高的精度,特别是对于权重。但计算和存储 S, Z 的开销更大。
为什么需要校准?
在静态量化和量化感知训练中,我们会需要校准集进行校准。
- 在量化感知训练中,我们通过校准集进行微调,并求出权重tensor 和 激活值的S,Z,然后在根据得到的S、Z进行量化
- 而在静态量化中,一旦模型训练完成,权重是固定的,因此我们可以离线地对权重进行量化(不需要校准集),但是激活值是动态的,他们完全依赖于当前输入的数据,因此对于不同的输入样本或不同的输入批次,同一层的激活值会发生变化,其数值范围(min, max)也会随之波动。因此在静态量化中我们需要通过校准集来确定激活值的 min、max
量化校准策略
上面讲到量化的过程中我们主要需要确定S,Z,对称量化的话只需要确定S。因此就涉及到怎么通过校准集来确定rmax,rmin。这一小节讲的量化的粒度是per-tensor
量化校准策略目的就是找到一个好的策略使得总的误差(舍入误差+裁剪误差)最小
- Min-max:记录下流经某个激活层的所有激活值的全局最小值(r_min)和全局最大值(r_max)。然后直接使用这两个值来计算 S 和 Z。
- 实现起来很简单,但是其对异常值敏感,如果校准数据中存在少数极端值,会导致 r_min 或 r_max 偏离主体数据的范围,使得计算出的 S(步长)过大。这会导致大部分处于密集区间的数值被量化到很少的几个整数值上,损失大量精度,从而会导致舍入误差很大,裁剪误差很小
该方法经常会用于对于权重的量化
- MSE: 选取一组候选的r_min,r_max,使用MSE计算 (计算量化-反量化之后的tensor) 和 (FP32的tensor)的均方误差,选择一个均方误差最小的一组r_min,r_max。
- 容易受这个tensor中那些大的值的影响,对大的值比较敏感,对小的值不敏感
- 百分位(Percentile):这种策略旨在显式地忽略掉分布两端的极端值。然后,不使用绝对的最小值和最大值,而是选择一个较小的百分比(例如 1% 或 0.1%)来截断分布的两端。例如,使用第 0.1 百分位的值作为 r_min,第 99.9 百分位的值作为 r_max 来计算 S 和 Z。
- 可以抵抗异常值的影响
- 百分位的阈值(如 99.9% vs 99.99%)是一个需要调整的超参数,选择不当也可能丢失重要信息。
- 该方法是一个不错的方法,可以平衡校准误差和舍入误差
- KL散度:通过校准集收集该流经该层的所有FP32激活值,并将其做成直方图(bin的选择不同也会影响T,因此会计算多个bin,例如(128-2048))。目的是找到一个阈值T,将[min,max]映射到[-T,T],使得KL(FP32||量化&反量化)的值最小,即让量化后的值和原始值的分布最相似
跨层均衡化(Cross-Layer Equalization)
量化误差中的一个常见的问题就是tensor中的元素大小不同,可能有一些元素很大,而一些元素很小,虽然量化校准策略中通过多种方法来试图找到clip误差 和round误差的平衡。但有时候差异很大,以至于难以找到平衡。对于这个问题,虽然对于采用更细粒度的量化粒度(例如per-channel量化)来说不太成问题,但对于更广泛使用的per-tensor量化仍然是一个大问题。
CLE:主要的思想就是通过引入可数学抵消的缩放因子(scaling factors)来调整相邻两个线性层(通常是卷积层或全连接层)之间的权重和偏置的数值范围(dynamic range),使得它们的范围更加均衡或相似。这个过程不会改变网络的原始数学计算结果,但会改变权重和偏置参数的具体数值。
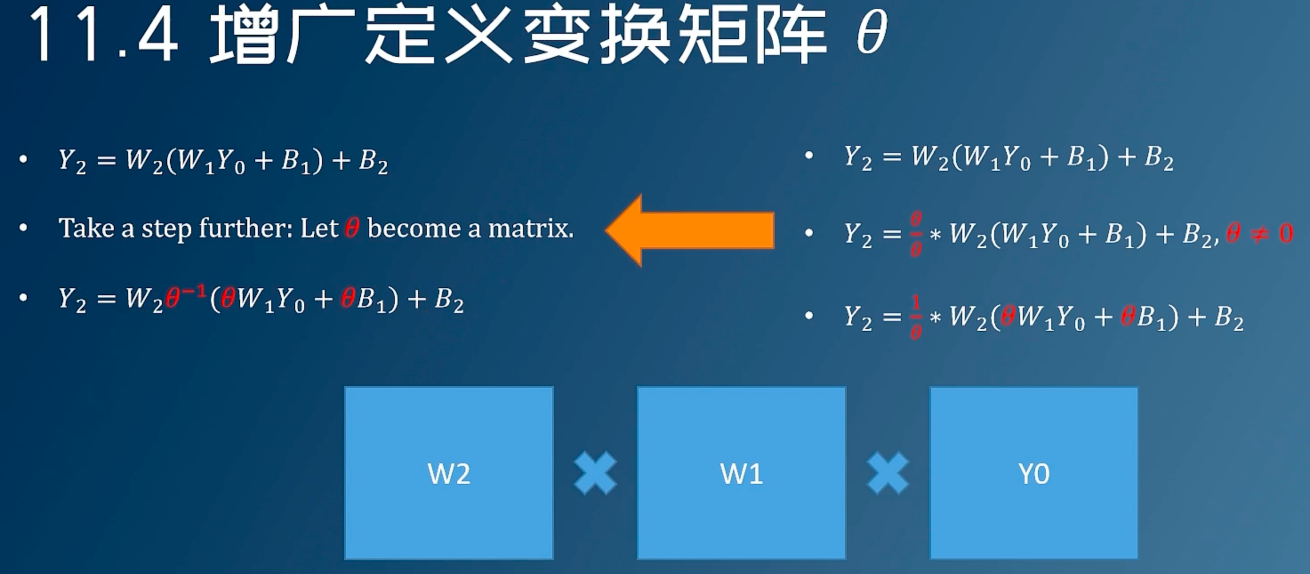
我们假设两个层,f为激活函数
h1 = f1(W1X + b1)h2 = f2(W2X + b1)
y = f2(W2f1(W1X + b1) + b2)
计算缩放因子s_i这个 s_i 的计算目标是平衡 ConvA 第 i 个输出通道的权重范围和 ConvB 第 i 个输入通道的权重范围。
ri(j) 是权重张量j的i通道的范围(即范围的最大绝对值,例如 [-33,22],则为33)
通过对权重的等价缩放,对前面的层除以s_i,后面前乘以s_i,这里假设 f(sx) = sf(x), s为常量 y = f2(W2Sf1(S − 1W1X + S − 1b1) + b2) 这样做可以让每一层的权重范围尽量地接近来避免一些tensor中的元素过大/过小的情况,从而提高量化的效果
限制:
上面我们我们的层中假设了f(sx) = sf(x),因此要想进行CLE,激活函数必须满足这个性质(例如RELU),sigmoid不满足这个性质,否则上述的对前面层的权重除以s_i,后面层的权重乘以s_i,这样得出的输出结果和不进行CLE之前是不等价的。
后训练量化(静态量化)
- 先在数据集上以FP32进行训练得到baseline模型
- 使用校准集(需要能代表真实输入数据分布的样本,不需要label)对FP32 baseline 模型进行校准,这一步主要是得到网络各层weights以及activation的数据分布特性(比如统计最大最小值)
- 根据得到的最大最小值计算出 S 、Z
- 使用第三步得到的S、Z对FP32 baseline模型进行量化
优缺点:
- 需要校准,校准数据需要具有代表性,否则误差可能会比较大
- 推理速度比动态量化更快
后训练量化(动态量化)
动态量化也是一种PTQ技术,在上面为什么需要校准中我们知道了静态量化为什么需要校准,而动态量化是通过预先量化模型的权重(weights),对于激活值,他不在推理前确定固定的量化参数,而是在推理时,根据当前输入数据流经每一层时实际产生的激活值范围,动态地计算该批次或该张量激活值的 S 和 Z,并进行量化。
优缺点:
- 不需要校准集,无需校准
- 推理速度速度比静态量化慢
一般来说RNN、transformer 使用动态量化、CNN使用静态量化
量化感知训练
量化感知训练(QAT)是一种模型量化技术。它的核心思想是在模型训练(或微调)过程中模拟量化操作带来的影响(如精度损失、数值范围变化等),让模型在训练时就“感知”到量化效应,并学习去适应这种效应,从而在最终将模型转换为低精度(如INT8)格式时,最大限度地减少精度损失。
具体来说:
- 先在数据集上以FP32精度进行模型训练,得到baseline模型
- 再在baseline模型中插入
伪量化节点来模拟量化操作,得到QTA模型,并使用校准集对QTA模型进行finetune - 伪量化节点会模拟推理时的量化过程并且保存finetune过程中计算得到的量化参数(S,Z)
- finetune完成后,使用上一步 中得到的量化参数对QAT模型进行量化得到INT8模型,并部署至推理框架中进行推理
使用校准集对QTA模型进行finetune时,可以分为
有标签的量化训练和无标签的量化训练无标签的量化训练:就是先使用带伪量化节点的QTA模型得到输出结果 O1,再去掉伪量化节点,即使用FP32的baseline模型得到O2,根据二者的结果,利用损失函数计算loss,再进行反向传播带标签的量化训练:就是先使用带伪量化节点的QTA模型得到输出结果 O1,根据这个输入原本的label 和 O1,利用损失函数计算loss,再进行反向传播
在量化感知训练的过程中,我们一般使用的是
校准集,校准集一般是从训练集中抽出一小部分数据,一般大约500-1000张图片(需要能代表真实输入数据分布的样本),在校准集上量化感知训练,因为网络本身已经训练好了,我们只是微调一下我们的网络(微调的时候learning_rate 不能太大)。下图就是无标签的量化训练,将输入分别输入进带
伪量化节点的网络和真实的浮点网络,根据二者的结果,利用损失函数计算loss,再进行反向传播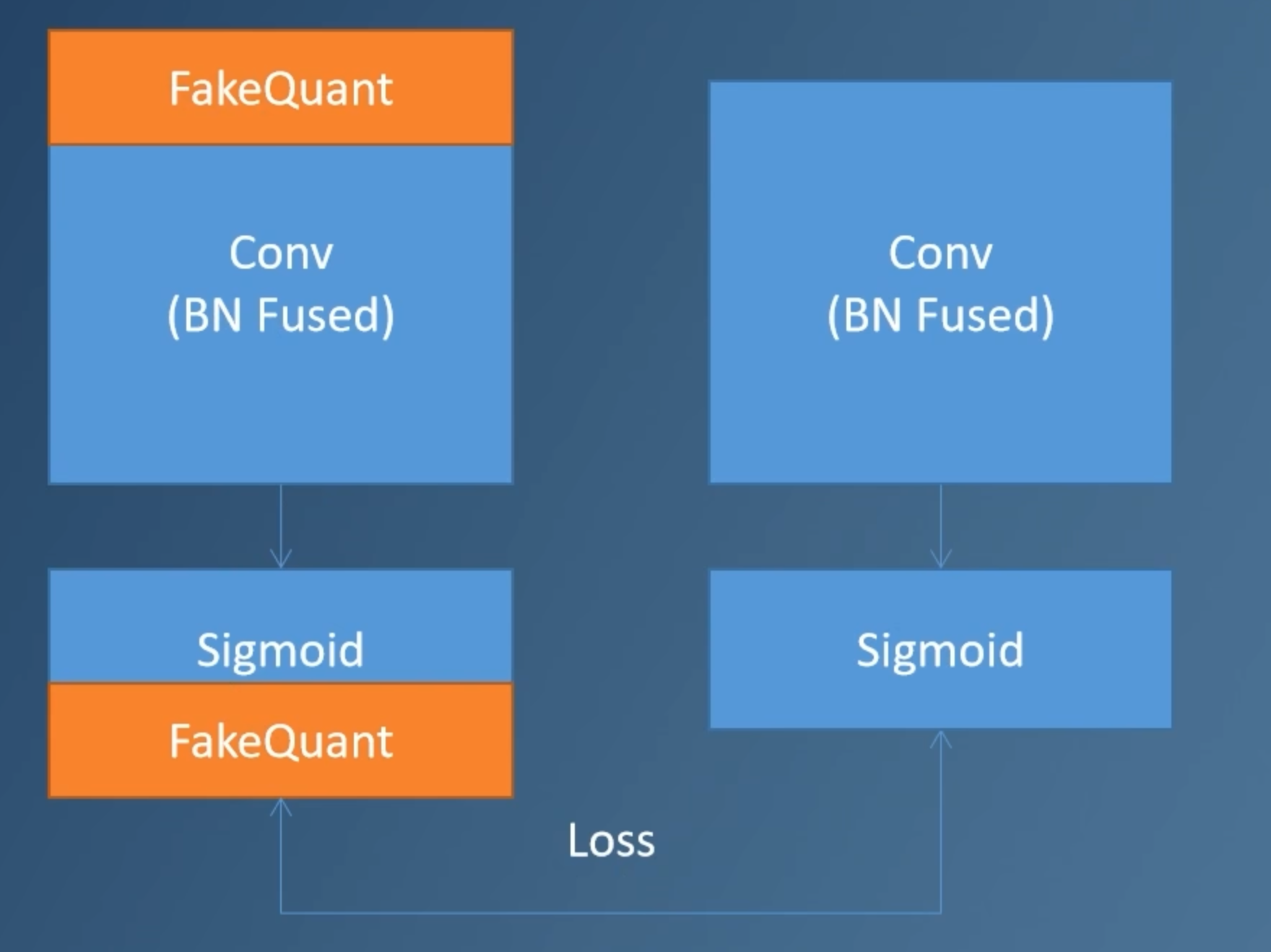
偏差校正(Bias correction)
偏差校正是一种PTQ技术,当我们进行量化的时候必然存在量化误差,即 Wq = W + △ W
因此 Y = Wq ⋅ X = (W + △ W) ⋅ X 因此 E(Y) = E(WX) + E( △ W ⋅ X) E(WX)是 FP32输出的期望,因此输出的期望的偏差就是E( △ W ⋅ X),因此在 E( △ W ⋅ X)不等于0时,输出的分布发生了变化。
为了纠正这个偏差,我们可以从输出中减掉这个偏差,即在bias中减去 E( △ W ⋅ X) ,即 b′ = b − E[ΔW * x]
偏差校正的计算方法有多种,其中最常见的两种方法是经验偏差修正和分析偏差修正。
- 经验偏差校正: 即通过校准数据集来对偏差矫正
- 将校准数据输入FP32模型,记录当前层输出值的均值
- 将相同的校准数据输入量化之后的模型,记录当前层输出的均值
- 计算二者的偏差得到 bias_error,计算 b′ = b − bias_error,并更新模型
分析偏差校正

自适应取整(AdaRound)
AdaRound是一种PTQ技术,根据下面的量化公式可以看出,正常的PTQ量化在舍入的时候采取的是四舍五入的舍入方式(称为最近邻取整),最近邻取整是在局部最小化单个权重值的量化误差(|原始值 - 量化后值|)。但是,模型最终的性能是由所有权重共同作用决定的。一个对单个权重来说局部最优的舍入决策,不一定对整个模型的最终输出(全局性能)是最优的。可能某个权重稍微“舍入得远一点”(不是最近邻),反而能更好地补偿其他权重舍入带来的误差,或者更好地保留对模型输出影响更大的信息。 q = clamp(round(r/S + Z), qmin, qmax) AdaRound 的核心思想是:对于每一个权重参数,不一定总是执行最近邻取整,而是根据该取整决策对最终模型输出(或一个代理损失)的影响,来自适应地决定是向上取整(round up)还是向下取整(round down)。
最佳实践
PTQ最佳实践
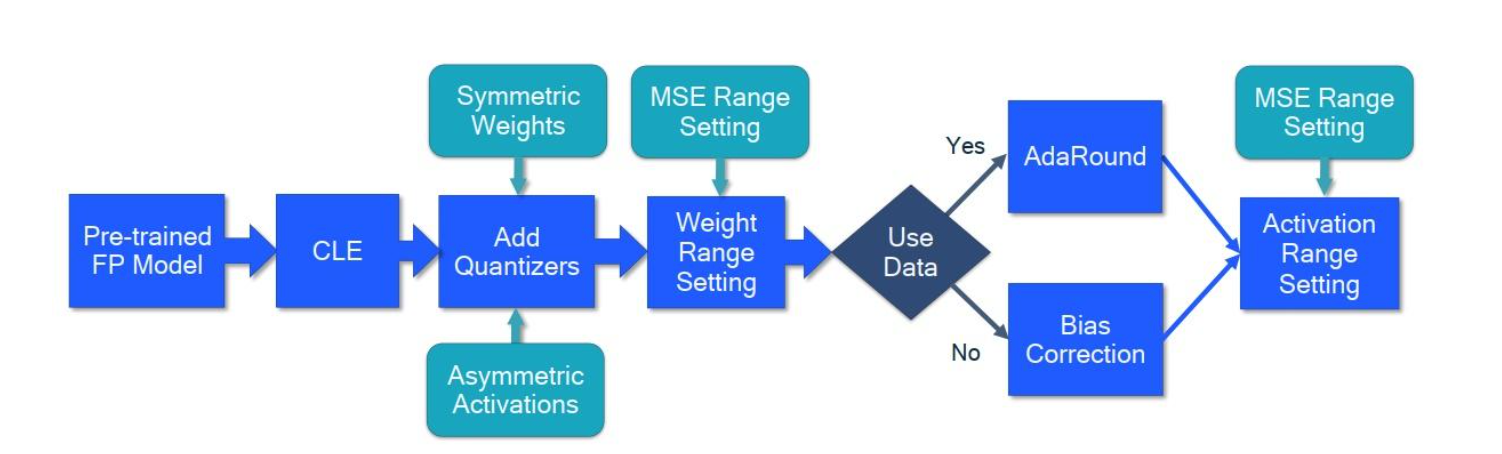
CLE 让模型更加好量化,对于具有深度可分离层的模型和per-tensor的粒度的量化比较有效
添加量化器,权重使用对称量化,激活使用非对称量化(当然有些推理框架不量化激活),同时可以使用per-channel的粒度来提高量化的效果
权重范围的设置:建议使用MSE的方式来设置权重的范围,如果采用per-channel的粒度,也可以使用min-max的方法
如果我们有小的校准集的话,接下来可以使用AdaRound来优化权重的舍入,尤其是在实现低比特权重(例如4bits)量化时
没有校准集的话,并且网络使用BN的话,可以使用分析偏差校正
最后一步确定网络中激活的量化范围,大多数层使用基于MSE的方法来确定激活值的范围,这样的话需要一个校准集来找到最小的MSE损失;或者可以使用基于BN的范围设置来实现一个完全无数据的流水线(data-free pipeline)
QAT的最佳实践
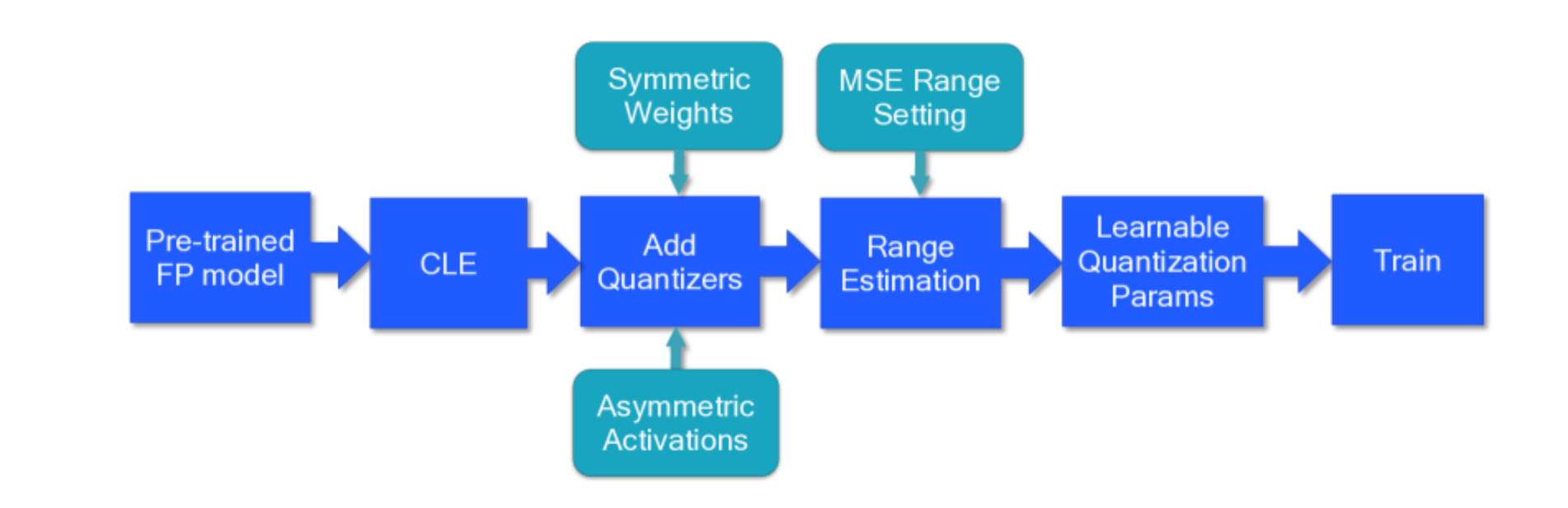
和PTQ类似,首先取FP32模型应用CLE,这一步对于遭受不平衡权重分布的模型,如 MobileNet 架构,是必要的。对于其他网络或在进行通道量化时,这一步可以是可选的
这一步和PTQ类似,添加量化器,权重使用对称量化,激活使用非对称量化(当然有些推理框架不量化激活),同时可以使用per-channel的粒度来提高量化的效果
在训练之前,我们必须初始化所有量化参数。更好的初始化将有助于加速训练并可能提高最终精度,尽管通常这种改进很小。一般来说,我们建议使用基于层间均方误差(MSE)的标准来设置所有量化参数。在特定情况下,对于按per-channel量化,可以使用最小-最大的方法来设置
直接学习量化参数,而不是在每个 epoch 更新它们,尤其是在处理低比特量化时,可以带来更高的性能。然而,在使用可学习量化器时,在设置任务优化器时需要特别注意。当使用 SGD 类型的优化器时,量化参数的学习率需要比网络的其他参数降低。如果我们使用具有自适应学习率的优化器,如 Adam 或 RMSProp,则可以避免学习率调整(因为这些优化器对学习率不那么敏感)。
图融合加速
为什么要图融合?
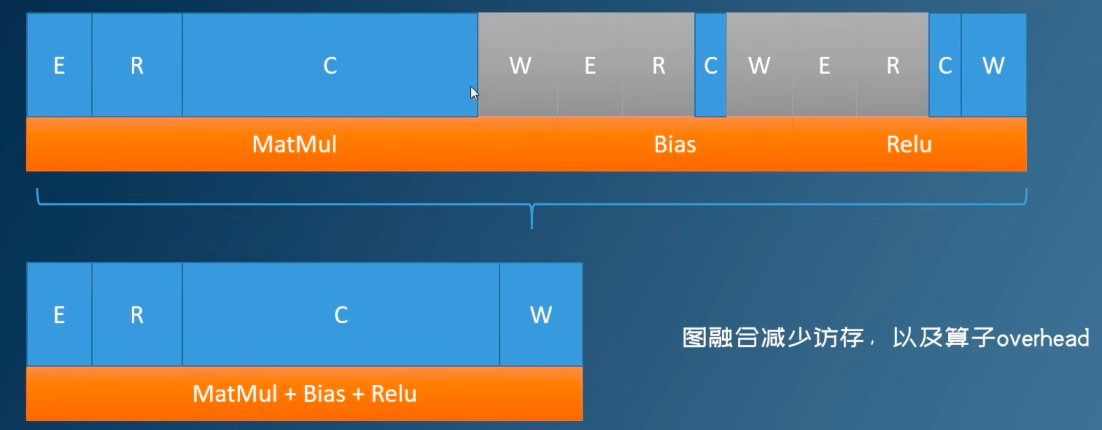
对于每个算子的运算,我们都需要进行这四个步骤:任务发射、读数据、计算、写数据
不进行图融合:

进行图融合:
常见的计算图优化:
激活函数的融合

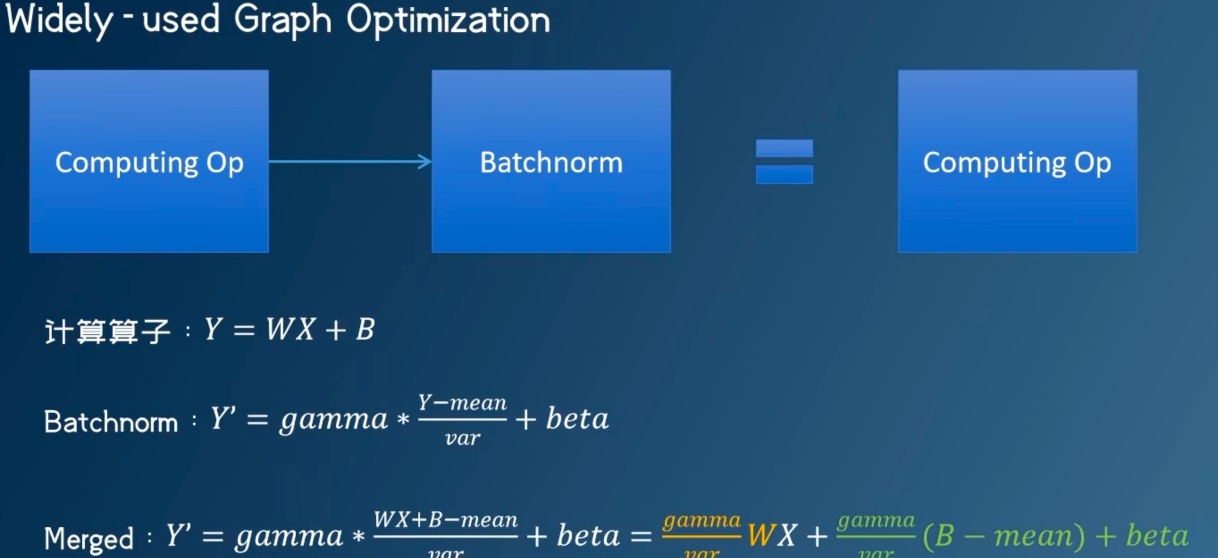
移除BN 和 Dropout
矩阵乘融合
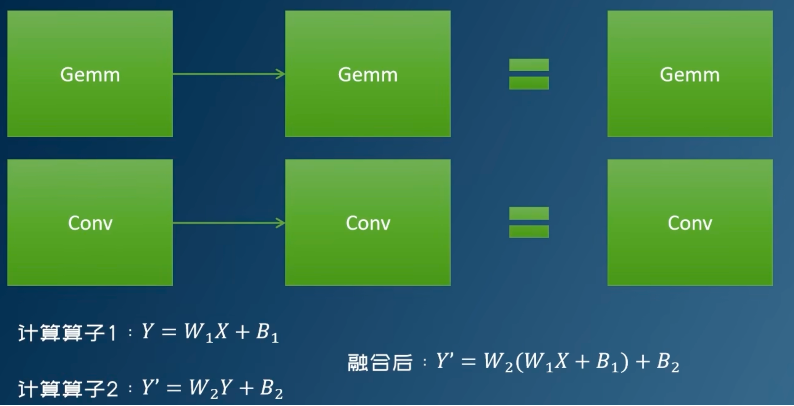
conv - add 融合


参考
王小二 中的有关量化白皮书的相关内容
A White Paper on Neural Network Quantization 本文很多内容都是基于这个量化白皮书的
- 本文作者: leftover
- 版权声明: 本文版权归leftover所有,如需转载清标明来源!