低秩分解

低秩分解旨在将一个高维、可能含有噪声低矩阵分解为两个/多个低秩句子的乘积。例如如果原始矩阵为M，那么我们希望找到两个低秩矩阵 A、B，使得M ≈ AB,这种近似方式在损失尽可能少的信息的同时，降低了数据的复杂性和计算量，常用于数据压缩，降维

特征值分解

假设A 为NxN的方阵 有 N个特征向量

因此根据线性代数中的知识 A = P ∧ P^− 1 其中 P的第i列为矩阵A的特征向量v_i , ∧ 为对角矩阵，对角线上的元素为对应的特征值。

再进一步，若A为对称矩阵，则其特征向量两两正交,因此存在一个正交矩阵Q,使得 A = Q ∧ Q^− 1 = Q ∧ Q^T

SVD 分解

SVD则可以认为是上述特征值分解在任意矩阵上的推广，即给定任意矩阵 A ∈ R^M × N ，可以被分解为: A = UΣV^T 其中U为 MxM的 正交矩阵， Σ 为MxN的对角矩阵，并且其对角元素非负，V^T 为 NxN的正交矩阵

Σ 中的元素被称为奇异值，U、V的列向量分别被称为矩阵A的左奇异向量和右奇异向量

我们通常会对 Σ 的对角元素进行排序使其满足 σ₁ ≥ σ₂ ≥ ⋯ ≥ σ_R

全连接层SVD分解

全连接层将N维特征经过线性映射到M为特征，因此在FC层中，其权重矩阵W是一个MxN的矩阵。因此根据上面的SVD分解，W = UΣV^T。

为了对权重矩阵W进行压缩，我们可以只保留W的最大K个奇异值来对W进行近似 其中

为了进一步压缩，我们可以将 中的元素乘到 Ũ 和/或 Ṽ 中，如下，这样的话可以只需要对 进行存储和参与计算。

SVD分解之前W的存储和计算复杂度为O（MN）， SVD分解之后降低为O((M+N)K),其中K是一个很小的数

为了平衡SVD分解之后的误差和计算/存储效率，需要选择一个合适的K，以到达效率和精度之间的平衡

如图所示：

SVD分解

保留最大的r=3个奇异值

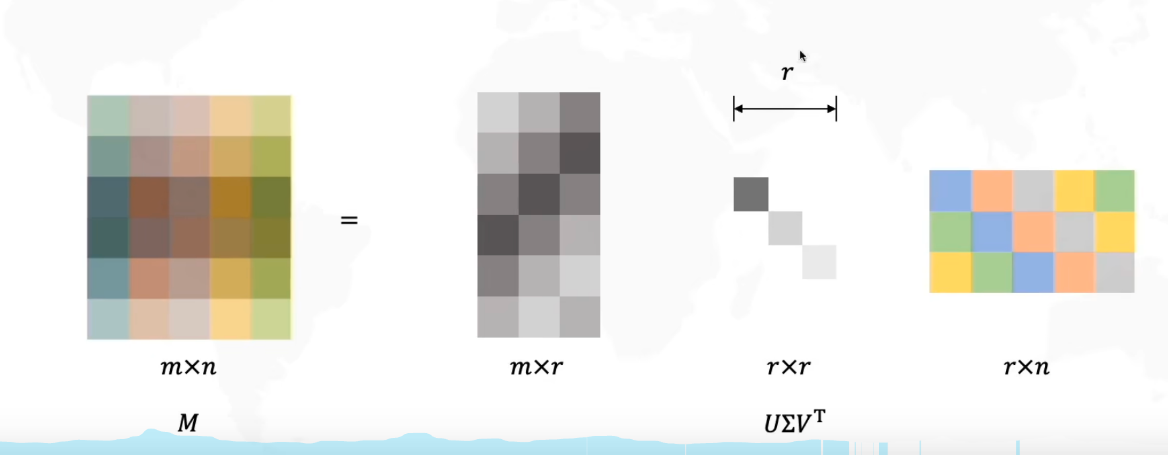
卷积层SVD分解

上述全连接层的权重参数是一个二维矩阵，可以很轻易地进行奇异值分解，而卷积层的权重参数为 W ∈ R^{N × C × D × D} 是一个四维的张量,不好进行奇异值分解,因此我们需要将其展开为二维矩阵，再对展开的二维矩阵进行SVD分解。N为输出通道数，C为输入通道数，D为卷积核的大小（通常卷积核的长宽相等），

将四维张量展开为二维矩阵的方式有很多，每一种展开都对应一种SVD分解方式，但是基本原理都差不多

通道分解

对输入通道或输出通道进行重排，得到二维矩阵，再进行SVD分解。以下以输出通道为例，将W转为二维矩阵 W ∈ ℝ^{N × (CDD)} ，并进行奇异值分解 W ≈ UΣV^T 其中 U ∈ ℝ^N × R、Σ ∈ ℝ^R × R、V^T ∈ ℝ^{R × (CDD)}

这样的话，可以将权重张量W表示对卷积层转为两个以 U 和 V 为参数的卷积层（Σ 可以被吸收到 U 和/或V中）

完成分解之后，将U 转为 U ∈ ℝ^{N × R × 1 × 1} ， 将V转为V ∈ ℝ^{R × C × D × D} 的两个卷积。

原来的卷积的参数量为O(NCDD) ,分解之后的卷积的参数量为O(NR+RCDD)

空间分解

空间分解则是将形状为NxCxDxD的张量在卷积核的空间维度上进行展开，即W ∈ ℝ^{(N × D)(C × D)}

然后对W进行SVD分解，得到 W ≈ UΣV^T 其中U ∈ ℝ^{N × D × R}、Σ ∈ ℝ^R × R、V^T ∈ ℝ^{R(C × D)}

最后将U 转为 U ∈ ℝ^{N × R × 1 × D} ， 将V 转为 V ∈ ℝ^{R × C × D × 1}

其实本质上和通道分解差不多，只是分解的角度不一样，大部分的东西都是一样的

张量分解

上述对卷积层的权重参数进行分解是先将其展开为2D矩阵，再使用SVD分解方式对2D矩阵进行分解。而张量分解则是直接对整个张量进行分解，常见的分解方法有 Tucker 分解、CP分解 、BTD分解 则是用公式、定理直接对整个张量分解，各个方法都大差不差

参考

深度神经网络高效计算 的低秩分解一节